nLab Majorana dimer code
Context
Quantum systems
-
quantum algorithms:
Contents
Idea
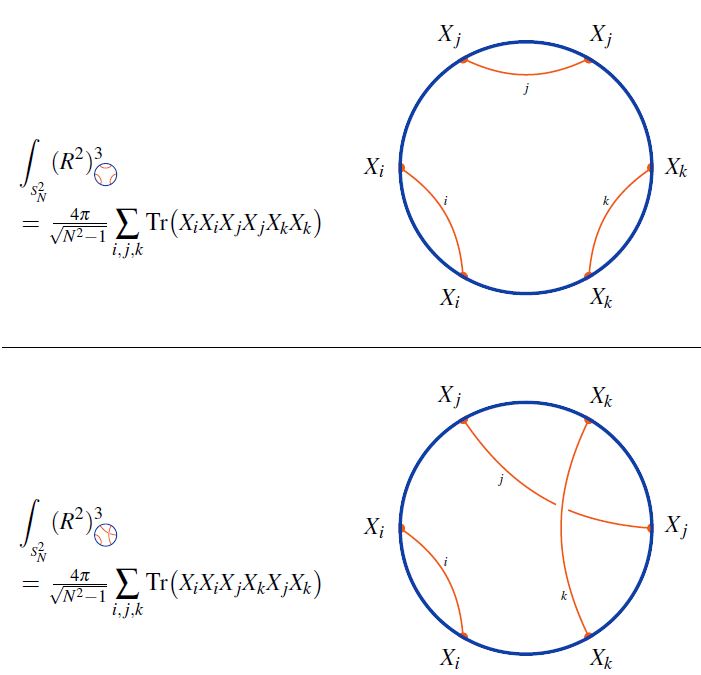
A class of quantum error correcting codes whose code subspaces are the images of linear maps given by tensor networks of the shape of round chord diagrams with chords acting as Majorana dimers.
The Majorana dimer code subsumes the HaPPY code:
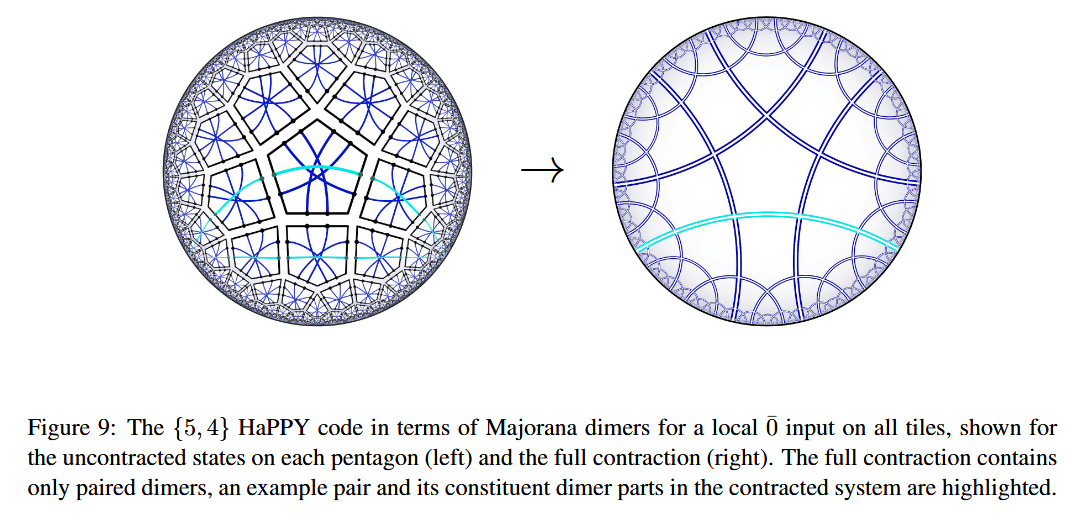
and makes the nature of holographic entanglement entropy particularly manifest (see there for more).
Related concepts
References
General
Due to:
- Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting code, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
based on:
- Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Holography and criticality in matchgate tensor networks, Science Advances 5, eaaw0092 (2019) (arXiv:1711.03109, doi:10.1126/sciadv.aaw0092)
Review in:
- Alexander Jahn, Jens Eisert, Holographic tensor network models and quantum error correction: A topical review (arXiv:2102.02619)
See also:
-
Alexander Jahn, Zoltán Zimborás, Jens Eisert, Central charges of aperiodic holographic tensor network models, Phys. Rev. A 102, 042407 (arXiv:1911.03485)
-
Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)
Chord diagrams and weight systems in Physics
The following is a list of references that involve (weight systems on) chord diagrams/Jacobi diagrams in physics:
-
In quantum many body models for for holographic brane/bulk correspondence:
For a unifying perspective (via Hypothesis H) and further pointers, see:
-
Hisham Sati, Urs Schreiber, Differential Cohomotopy implies intersecting brane observables, Adv. Theor. Math. Phys. 26 4 (2022) [doi:10.4310/ATMP.2022.v26.n4.a4arXiv:1912.10425]
-
David Corfield, Hisham Sati, Urs Schreiber: Fundamental weight systems are quantum states Lett. Math. Phys. 113 112 (2023) [arXiv:2105.02871, doi:10.1007/s11005-023-01725-4]
-
Carlo Collari, A note on weight systems which are quantum states, Can. Math. Bull. 66 4 (2023) [doi:10.4153/S0008439523000206, arXiv:2210.05399]
Review:
- Carlo Collari, Weight systems which are quantum states, talk at QFT and Cobordism, CQTS (Mar 2023) web, pdf
In Chern-Simons theory
Since weight systems are the associated graded of Vassiliev invariants, and since Vassiliev invariants are knot invariants arising as certain correlators/Feynman amplitudes of Chern-Simons theory in the presence of Wilson lines, there is a close relation between weight systems and quantum Chern-Simons theory.
Historically this is the original application of chord diagrams/Jacobi diagrams and their weight systems, see also at graph complex and Kontsevich integral.
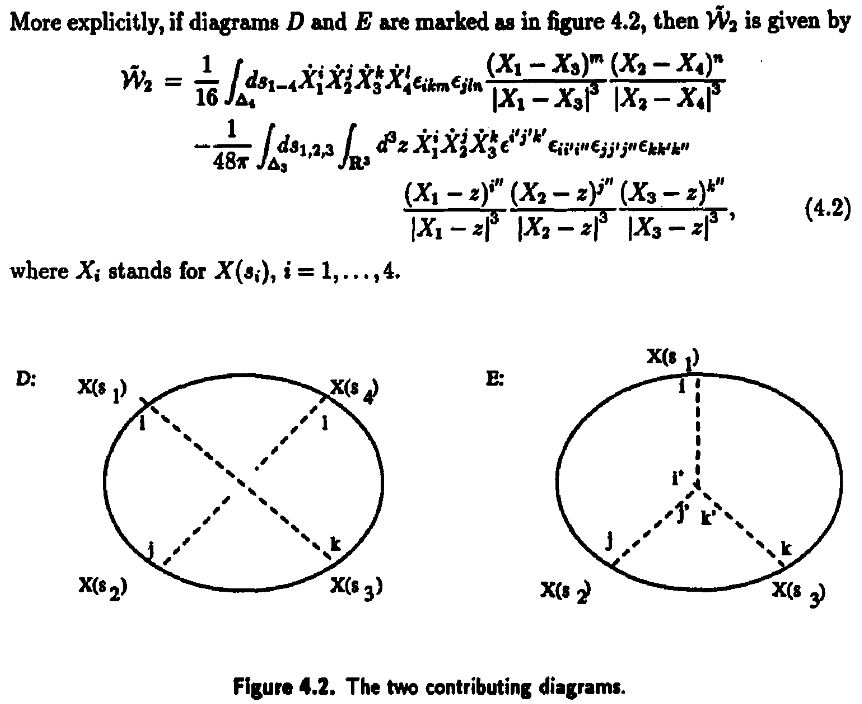
-
Dror Bar-Natan, Perturbative aspects of the Chern-Simons topological quantum field theory, thesis 1991 (spire:323500, proquest:303979053, BarNatanPerturbativeCS91.pdf)
-
Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)
-
Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arxiv:q-alg/9603010)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Algebraic structures on graph cohomology, Journal of Knot Theory and Its Ramifications, Vol. 14, No. 5 (2005) 627-640 (arXiv:math/0307218)
Reviewed in:
- Ismar Volić, Section 4 of: Configuration space integrals and the topology of knot and link spaces, Morfismos, Vol 17, no 2, 2013 (arxiv:1310.7224)
Applied to Gopakumar-Vafa duality:
- Dave Auckly, Sergiy Koshkin, Introduction to the Gopakumar-Vafa Large Duality, Geom. Topol. Monogr. 8 (2006) 195-456 (arXiv:0701568)
See also
-
Marcos Mariño, Chern-Simons theory, matrix integrals, and perturbative three-manifold invariants, Commun. Math. Phys. 253 (2004) 25-49 (arXiv:hep-th/0207096)
-
Stavros Garoufalidis, Marcos Mariño, On Chern-Simons matrix models (pdf, pdf)
For single trace operators in AdS/CFT duality
Interpretation of Lie algebra weight systems on chord diagrams as certain single trace operators, in particular in application to black hole thermodynamics
- Micha Berkooz, Prithvi Narayan, Joan Simón, Section 2.1 of Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
In , JT-gravity/SYK-model
Discussion of (Lie algebra-)weight systems on chord diagrams as SYK model single trace operators:
-
Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order , JHEP 04 (2018) 146 (arXiv:1801.02696)
-
Yiyang Jia, Jacobus J. M. Verbaarschot, Section 4 of: Large expansion of the moments and free energy of Sachdev-Ye-Kitaev model, and the enumeration of intersection graphs, JHEP 11 (2018) 031 (arXiv:1806.03271)
-
Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
following:
- László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)
which in turn follows
- Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

With emphasis on the holographic content:
-
Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)
-
Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large Double-Scaled SYK, 2019 (pdf)
-
Micha Berkooz, Mikhail Isachenkov, Prithvi Narayan, Vladimir Narovlansky, Quantum groups, non-commutative , and chords in the double-scaled SYK model [arXiv:2212.13668]
-
Herman Verlinde, Double-scaled SYK, Chords and de Sitter Gravity [arXiv:2402.00635]
-
Micha Berkooz, Nadav Brukner, Yiyang Jia, Ohad Mamroud, A Path Integral for Chord Diagrams and Chaotic-Integrable Transitions in Double Scaled SYK [arXiv:2403.05980]
and specifically in relation, under AdS2/CFT1, to Jackiw-Teitelboim gravity:
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)
-
Henry W. Lin, The bulk Hilbert space of double scaled SYK, J. High Energ. Phys. 2022 60 (2022) arXiv:2208.07032, doi:10.1007/JHEP11(2022)060
-
Henry W. Lin, Douglas Stanford, A symmetry algebra in double-scaled SYK arXiv:2307.15725
-
Micha Berkooz, Ohad Mamroud: A Cordial Introduction to Double Scaled SYK [arXiv:2407.09396]
-
Adel A. Rahman, Leonard Susskind: -Chords, Wee-Chords, and de Sitter Space [arXiv:2407.12988]
In D/D-brane intersections
Discussion of weight systems on chord diagrams as single trace observables for the non-abelian DBI action on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):
-
Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)
-
Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)
-
Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)
-
Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)
As codes for holographic entanglement entropy
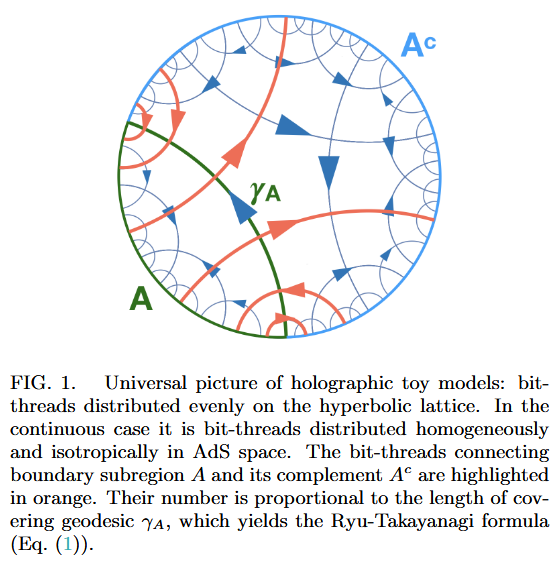
Chord diagrams encoding Majorana dimer codes and other quantum error correcting codes via tensor networks exhibiting holographic entanglement entropy:
-
Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting code, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
-
Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)

For Dyson-Schwinger equations
Discussion of round chord diagrams organizing Dyson-Schwinger equations:
-
Nicolas Marie, Karen Yeats, A chord diagram expansion coming from some Dyson-Schwinger equations, Communications in Number Theory and Physics, 7(2):251291, 2013 (arXiv:1210.5457)
-
Markus Hihn, Karen Yeats, Generalized chord diagram expansions of Dyson-Schwinger equations, Ann. Inst. Henri Poincar Comb. Phys. Interact. 6 no 4:573-605 (arXiv:1602.02550)
-
Paul-Hermann Balduf, Amelia Cantwell, Kurusch Ebrahimi-Fard, Lukas Nabergall, Nicholas Olson-Harris, Karen Yeats, Tubings, chord diagrams, and Dyson-Schwinger equations [arXiv:2302.02019]
Review in:
- Ali Assem Mahmoud, Section 3 of: On the Enumerative Structures in Quantum Field Theory (arXiv:2008.11661)
Other
Appearance of horizontal chord diagrams in discussion of neutrino interactions in supernovae:
- Duff Neill, Hanqing Liu, Joshua Martin, Alessandro Roggero: Scattering Neutrinos, Spin Models, and Permutations [arXiv:2406.18677]
Last revised on May 14, 2021 at 14:18:16. See the history of this page for a list of all contributions to it.